指定した分布に従う乱数の生成アルゴリズムについて

作成: 令和2年12月27日, 編集: 12月30日, 創価大学理工学部　畝見達夫

正規分布

Box-Müller 法によれば， 平均値 \(\mu = 0\)，標準偏差 \(\sigma = 1\) の正規分布に従う互いに独立な乱数 \(x_1\) と \(x_2\) を，区間 \([0,1)\) の互いに独立な一様乱数 \(R_1\) と \(R_2\) から，以下の式で求められる。 \[ x_1 = r \sin\theta, ~~ x_2 = r\cos\theta. ~~ \mbox{ただし} ~ r = \sqrt{-2 \ln R_1}, ~~ \theta = 2\pi R_2 \]

これを実現する C 言語のコードは，たとえば以下のように書ける。

double random_guassian(void) {
    static double z = 0.;
    static int secondTime = FALSE;
    if (secondTime) { secondTime = FALSE; return z; }
    else {
        secondTime = TRUE;
        double r = sqrt(-2. * log(random() / (double)0x7fffffff)),
            th = random() / (double)0x7fffffff * M_PI * 2.;
        z = r * cos(th);
        return r * sin(th);
    }
}

\([-1,1]\) 区間への補正

上記の乱数 \(x\) を指定された区間 \([-1,1]\) に収めるため，以下のような補正関数を用意する。 \[ \mbox{N}(x) = \left\{\begin{array}{ll}-2-u & \mbox{if} ~ u < -1\\ u & \mbox{if} ~ -1 \leq u \leq 1 \\ 2 - u & \mbox{if} ~ 1 < u\end{array}\right. ~~ \mbox{ただし} ~ u =\frac{x}{3} \]

尖度

通常の尖度は4次モーメントで表されるが，ここでは \([-1,1]\) 区間のパラメータ \(k\) により制御する。\([-1,1]\)区間の乱数 \(x\) に対する補正関数は以下のとおり。 \[ \mbox{K}(x,k) = \left\{\begin{array}{ll} (1+x)^\beta - 1 & \mbox{if} ~ x < 0 \\ 1 - (1-x)^\beta & \mbox{if} ~ x \geq 0\\ \end{array}\right. ~~ \mbox{ただし} ~ \beta = 2^{-k} \]

\(y=\mbox{K}(x,k)\) は，\((-1,-1), (0,0), (1,1)\) をとおる原点 \((0,0)\) の周りに点対称で，\(x\in[-1,1]\) の区間では単調に増加する曲線であり，\(x\) についての微分した導関数 \(\mbox{K}'(x,k)\) は，\(\mbox{K}'(0,k)=2^{-k}\)， \[ \mbox{K}'(-1,k)=\mbox{K}'(1,k)=\left\{\begin{array}{ll} 0 & \mbox{if} ~ k < 0\\ 1 & \mbox{if} ~ k = 0\\ +\infty & \mbox{if} ~ k > 0\\ \end{array}\right. \] である。

歪度

通常の歪度は３次モーメントで表されるが，ここでは区間 \((0,1)\) 内の最頻値 \(m\) を与え，それを満足するよう，区間 \([0,1]\) の乱数 \(x\) を補正する以下の関数を用意する。 \[ \mbox{M}(x, m) = \frac{\alpha x}{1-(1-\alpha)\:x} ~~ \mbox{ただし} ~ \alpha = \frac{m}{1-m} \]

\(m\)を固定したとき \(y=\mbox{M}(x,m)\)で表される \(x,y\) 平面上の曲線は，\(y = 1/x\)の曲線と相似で，原点 \((0,0)\) と 点 \((1,1)\) をとおり，直線 \(y=1-x\) に対し対称となる。

合成された補正

上記の補正関数 \(\mbox{N, K, M}\) を用いて，区間 \([l,h]\)，最頻値 \(m\)，尖度の係数 \(k\) のベル型の分布関数に従う乱数を \(\mbox{N}(0,1)\) の標準正規分布に従う乱数 \(x\) から以下の式で求める。

\[ \mbox{C}(x,l,h,m,k) = (h-l)\:\mbox{M}\left(\frac{\mbox{K}(\mbox{N}(x),k)+1}{2},\frac{m-l}{h-l}\right)+l \]

他の乱数と相関性のある乱数の生成

上記の \(\mbox{N, M}\) を用いて生成された区間 \([0,1)\) の乱数 \(x\) と，相関性のある区間 \([0,1)\) の乱数を，以下の関数 \(\mbox{F}\) により生成する。

\[ \mbox{F}(x,m_x,m_y,c)=\left\{\begin{array}{ll} 1-f(1-m_y,-c) & \mbox{if}~c<0\\ f(m_y,c) & \mbox{if}~c\geq 0 \end{array}\right. \] \[ f(m_y,c)=(1-c)\left(\mbox{M}\left(\frac{\mbox{N}(R)+1}{2}, \gamma\:y + (1-\gamma)\:m_y\right)-y\right) \] \[ y = \frac{m_y (1-m_x)\:x}{m_x(1-m_y)-(m_x-m_y)\:x} \]

ここで，\(c\) は区間 \([-1,1]\) 内の相関係数，\(\gamma=0.1\)，\(m_x, m_y\) はそれぞれ元の乱数の最頻値と新たに生成する乱数の最頻値，\(R\) は \(\mbox{N}(0,1)\) の標準正規分布に従う乱数である。

検証のためのコード

上記の関数が正しく働くことを確認するため，processing を用いて以下のコードを作成した。 末尾に出力結果を示す。

float mX = 0.9, mY = 0.1;  // mode as skewness (0, 1)
float kX = 0., kY = 0.; // kurtosis
float cor = 0.5; // correlation between x and y
//
int nBins = 100;
int cntX[] = new int[nBins], cntY[] = new int[nBins];
int maxCntX, maxCntY, nn;
void reset() {
  maxCntX = maxCntY = nn = 0;
  for (int i = 0; i < nBins; i ++) cntX[i] = cntY[i] = 0;
}
void setup() {
  size(800, 400);
  noStroke();
  setupGUI();
  reset();
}
int countH(float v, int cnt[], int maxCnt) {
    int idx = floor(v * nBins);
    if (idx >= nBins) idx = nBins - 1;
    else if (idx < 0) idx = 0;
    cnt[idx] ++;
    return (cnt[idx] <= maxCnt)? maxCnt : cnt[idx];
}
float myRandom(float m, float k) {
    float x = randomGaussian() / 3.;
    if (x < -1.) x = -2. - x;
    else if (x > 1.) x = 2. - x;
    if (k != 0.) {
      float b = pow(2., -k);
      x = (x < 0.)? pow(1. + x, b) - 1. : 1. - pow(1. - x, b);
    }
    x = (x + 1.) / 2.;
    float a = m / (1. - m);
    return a * x / ((a - 1) * x + 1);
}
void drawHist(int cnt[], int maxCnt) {
  int w = (width-height)/nBins;
  for (int i = 0; i < nBins; i ++) {
    rect(i*w, height/2-1, w, -cnt[i]*height/2/maxCnt);
  }
}
void draw() {
  if (nn >= 100) return;
  if ((nn ++) == 0) background(16,8,90);
  pushMatrix();
  translate(width - height, 0);
  fill(255, 255, 255, 32);
  float absC = abs(cor);
  float mYY = (cor < 0.)? 1 - mY : mY;
  for (int i = 0; i < 1000; i ++) {
    float x = myRandom(mX, kX);
    maxCntX = countH(x, cntX, maxCntX);
    float y = mYY * (1 - mX) * x / (mX * (1 - mYY) - (mX - mYY) * x);
    y += (myRandom(y*.1+mYY*.9, kY) - y) * (1 - absC);
    if (cor < 0.) y = 1 - y;
    maxCntY = countH(y, cntY, maxCntY);
    rect(x * height, (1 - y) * height, 3, 3);
  }
  popMatrix();
  fill(#440000); rect(0,0,width-height,height/2);
  fill(#333300); rect(0,height/2,width-height,height/2);
  fill(255,255,255,180);
  drawHist(cntX, maxCntX);
  pushMatrix();
  translate(0, height/2);
  drawHist(cntY, maxCntY);
  popMatrix();
}

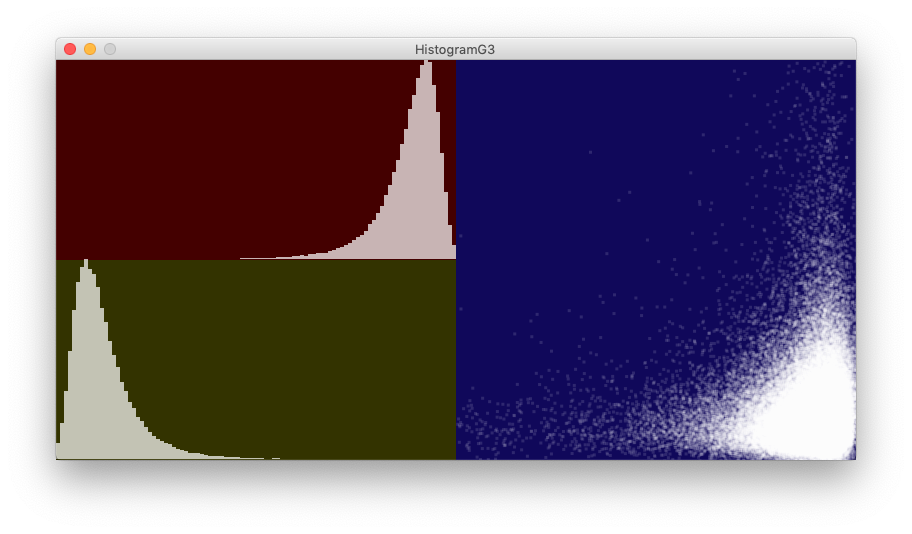
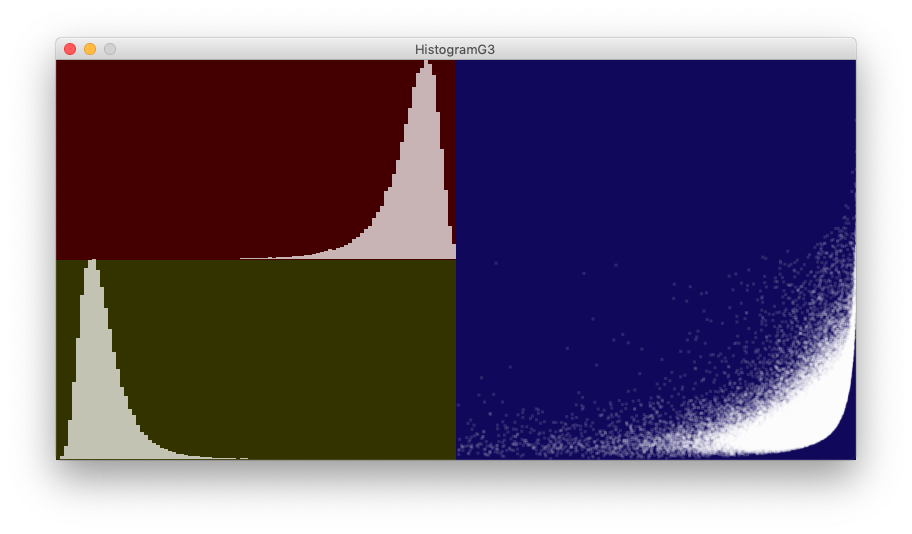
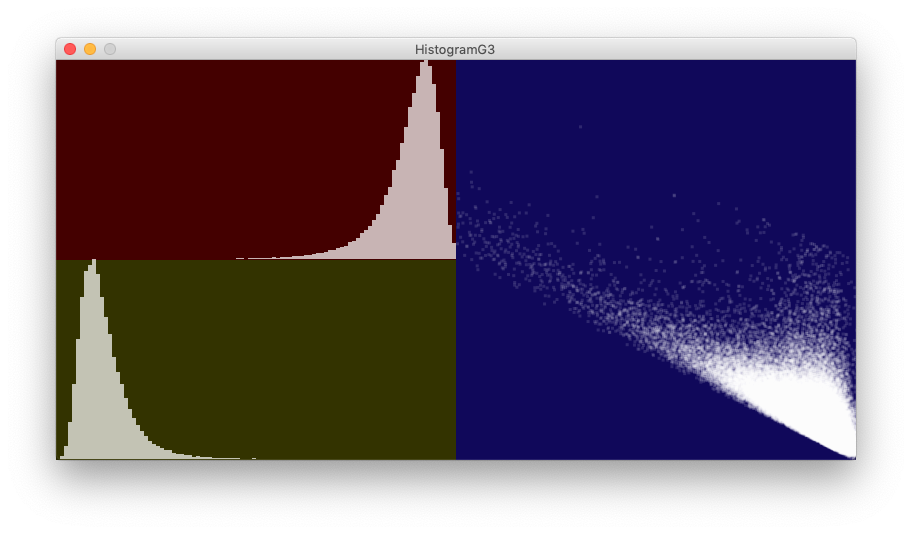
下の各図中，左上は元の乱数 \(x\) のヒストグラム，左下は生成した乱数 \(y\) のヒストグラム，右は横軸に \(x\) 縦軸に \(y\) をとった散布図である。いずれも最頻値は \(m_x = 0.9, m_y = 0.1\)，相関係数は上から \(0, 0.5, -0.5\) である。